Tree systems
From Supply Chain Management Encyclopedia
Russian: Древовидная структура
Consider a tree system[1]. The overall approach of the last section for series systems works here too. Actually, the approach works even for fully general systems, but only under a severe restriction involving leadtimes, as explained below. Also, the notation and analysis become more complex in the general case. Focus on tree systems.
Let formalize the network expressing the system's structure: It is a directed graph, specified by the pair of sets  . The nodes
. The nodes  represent the items;
represent the items;  is the number of items. The arcs
is the number of items. The arcs  describe the supply-demand or input-output relations. An arc from
describe the supply-demand or input-output relations. An arc from  to
to  denoted
denoted  , means that some of item
, means that some of item  is used to produce or supply item
is used to produce or supply item  (If there are several
(If there are several  with
with  , then all the inputs
, then all the inputs  are required for item
are required for item  ).
).
This graph is connected but acyclic; no group of items is independent of the others, and no item is used, directly or indirectly, to produce itself. One can number the items so that  whenever
whenever  . If
. If  , we say
, we say  is an (immediate) predecessor of
is an (immediate) predecessor of  and
and  is a successor of
is a successor of  .
.
Define
 -- set of predecessors of
-- set of predecessors of 
 -- set of successors of
-- set of successors of 
These sets list each item's immediate inputs and outputs. A start item is one with no predecessor, and an end item is one with no successor. Only start items receive supplies from outside the system; in a production setting they represent the raw materials. Only end items have exogenous demands.
In these terms an assembly system has one end item  , and each
, and each  has only one successor. An item may have several predecessors, however (unlike a series system). A distribution system, conversely, has one start item 1, and each
has only one successor. An item may have several predecessors, however (unlike a series system). A distribution system, conversely, has one start item 1, and each  has only one predecessor. An item may have several successors. The official definition of a tree system is a bit more intricate: Ignoring the directions of the arcs for the moment, the undirected network has no circuits; in other words, there is a unique (undirected) path connecting any two nodes. Provided this condition holds, an item may have several predecessors and successors. In all these cases the number of arcs is precisely
has only one predecessor. An item may have several successors. The official definition of a tree system is a bit more intricate: Ignoring the directions of the arcs for the moment, the undirected network has no circuits; in other words, there is a unique (undirected) path connecting any two nodes. Provided this condition holds, an item may have several predecessors and successors. In all these cases the number of arcs is precisely  .
.
The cost factors 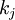 and
and  have the same meaning as in a series system, as do the local inventories
have the same meaning as in a series system, as do the local inventories  . Also, let
. Also, let  -- demand rate for item
-- demand rate for item  .
.
Only an end item may have  .
.
Contents |
Leadtimes and Quantity Units
Each arc  has an associated leadtime
has an associated leadtime  . Also, each start item
. Also, each start item  has order leadtime
has order leadtime 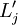 . These are non-negative constants. The corresponding zero-leadtime system has the same data, except all
. These are non-negative constants. The corresponding zero-leadtime system has the same data, except all  and
and 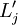 are 0.
are 0.
Consider some item  with several predecessors. The
with several predecessors. The  may include item-specific transportation times as well as assembly time, so in general the
may include item-specific transportation times as well as assembly time, so in general the  need not be equal over
need not be equal over  . Now, for a batch of
. Now, for a batch of  to be finished and available at time
to be finished and available at time 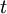 , a corresponding batch of item
, a corresponding batch of item  must be released at time
must be released at time  from every
from every  . It makes no sense to speak of placing an order for item
. It makes no sense to speak of placing an order for item  at a certain time if these
at a certain time if these  are different. Rather, the key events are now the departure and arrival times of batches on specific arcs. The inventory
are different. Rather, the key events are now the departure and arrival times of batches on specific arcs. The inventory  depends on all arrivals to and departures from
depends on all arrivals to and departures from  .
.
Echelons and Echelon Inventories
Echelon  comprises item
comprises item  itself, its successors, their successors, and so on. That is, echelon
itself, its successors, their successors, and so on. That is, echelon  includes
includes  and all subsequent items which use
and all subsequent items which use  as input, directly or indirectly.
as input, directly or indirectly.
The echelon inventory of item  is all the inventory in echelon
is all the inventory in echelon  , and its echelon demand rate is the total demand over items in echelon
, and its echelon demand rate is the total demand over items in echelon  . These quantities can be computed recursively, starting with the end items:
. These quantities can be computed recursively, starting with the end items:


The echelon holding cost is

In an assembly system, for example, echelon  comprises the items along the path from
comprises the items along the path from  to
to  , each
, each  is just
is just  , and, if
, and, if  is the (unique) element of
is the (unique) element of  ,
,

As in systems with linear structure, the total holding-cost rate at time 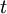 is again
is again

Policy Characteristics
Stationary-interval policies are not necessarily dominant, as in systems with linear structure. Still, they are convenient, and, as shown below, they do perform well.
A nested policy is one where an order for item i triggers an order for each of its successors, and hence throughout echelon  . In an assembly system, nested policies dominate others, as in a series system. Otherwise, nested policies need not be dominant. For example, consider the simple distribution system shown in Figure 1, where a warehouse (item 1) supplies two retailers (items 2 and 3). Suppose
. In an assembly system, nested policies dominate others, as in a series system. Otherwise, nested policies need not be dominant. For example, consider the simple distribution system shown in Figure 1, where a warehouse (item 1) supplies two retailers (items 2 and 3). Suppose  the
the  are equal,
are equal,  , but
, but  is much larger than
is much larger than  and
and  . It makes sense to order items 1 and 2 relatively often, but item 3 less frequently. (Since item 1 sometimes orders when 3 does not, such a policy is not nested.) Under a nested policy the system either incurs the cost
. It makes sense to order items 1 and 2 relatively often, but item 3 less frequently. (Since item 1 sometimes orders when 3 does not, such a policy is not nested.) Under a nested policy the system either incurs the cost  too often or carries too much inventory (at 1 or 2) to supply stage 2.
too often or carries too much inventory (at 1 or 2) to supply stage 2.
Nevertheless, some situations require a nested policy, not because it is less costly as measured by the model, but rather because it is easier to implement. If so, we say the system is nested. This distinction is unnecessary, of course, for an assembly system. For now, we focus on nested tree systems only.
Consider a policy with all three properties. Redefine
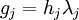

Then, the average cost of policy  is
is
![\,C(U)=\sum _{j}\left[\frac{k_{j} }{u_{j} } +\frac{1}{2} g_{j} u_{j} \right]](/images/math/a/a/e/aae67c0e6837e51458d5232ca3af0e5e.png)
Fig. 1. Simple distribution system.
The problem of choosing the best such policy, becomes:
![\,\min C(U)=\min \sum _{j}\left[\frac{k_{j} }{u_{j} } +\frac{1}{2} g_{j} u_{j} \right]](/images/math/0/f/a/0fa083afbce88c4edcbdda3a96adc7a6.png)

 ,
,  -- integer,
-- integer,

References
- ↑ Zipkin P. (2000) Foundations of inventory management; The McGraw-Hill Companies, Inc.





