Planned backorders
From Supply Chain Management Encyclopedia
Russian: Задолженный заказ
Contents |
The Setting
Consider the Basic economic order quantity (EOQ) system, but relax the requirement that all demand be met from stock on hand[1]. All demand is ultimately filled, though perhaps after a delay. That is, demand not filled immediately is backordered. Any inventory on hand is used to fill demand; backorders accumulate only when a warehouse runs out of stock entirely.
Reorder-Point/Order-Quantity Policies
Define some functions and redefine some of those used in the EOQ model:
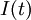 -- inventory at time
-- inventory at time 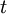 ;
;
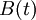 -- backorders at time
-- backorders at time 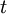 ;
;
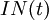 -- net inventory at time
-- net inventory at time 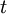 ,
, 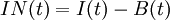 ;
;
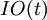 -- stock on order at time
-- stock on order at time 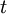 ;
;
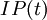 -- inventory position at time
-- inventory position at time 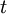 ,
, 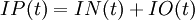 .
.
The new functions are 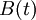 and
and 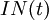 , and
, and 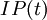 has a new meaning.
has a new meaning.
The net inventory 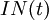 captures the information in both
captures the information in both 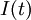 and
and 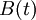 : At any given time, at least one of those two functions is zero, since we use any available stock to fill demand. Therefore,
: At any given time, at least one of those two functions is zero, since we use any available stock to fill demand. Therefore,
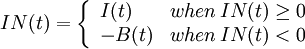
The definition of 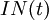 treats backorders as negative inventories, and indeed they function in this way: Between receipts of orders,
treats backorders as negative inventories, and indeed they function in this way: Between receipts of orders, 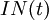 decreases at the constant rate
decreases at the constant rate 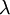 , regardless of whether
, regardless of whether 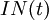 is positive or negative.
is positive or negative.
When an order arrives, 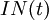 jumps up by precisely
jumps up by precisely 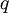 in all cases; some of the batch may be used to fill backorders, and the rest is added to inventory.
in all cases; some of the batch may be used to fill backorders, and the rest is added to inventory.
Thus, 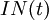 behaves much like
behaves much like 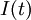 did before, when backorders were forbidden, while now
did before, when backorders were forbidden, while now 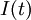 itself is more complex (
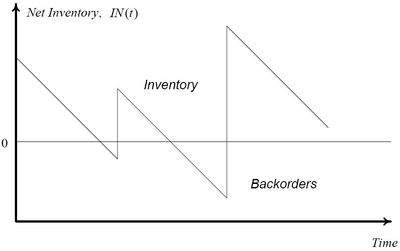
itself is more complex (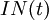 is sometimes called the inventory level.), fig. 1.
is sometimes called the inventory level.), fig. 1.
Consider,
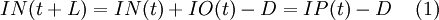
It is the conservation-of-flow law for this system: Between 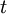 and
and 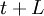 ,
, 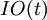 gets added to the net inventory, and
gets added to the net inventory, and 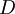 gets subtracted.
gets subtracted.
Thus, 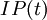 summarizes all the information needed to predict the net inventory a leadtime into the future.
summarizes all the information needed to predict the net inventory a leadtime into the future.
As in the EOQ model, assume that all orders are of the same size 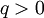 . The issue of when to order is now more complex. We need a second policy variable in addition to
. The issue of when to order is now more complex. We need a second policy variable in addition to 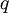 :
:
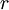 - reorder point (quantity-units)
- reorder point (quantity-units)
This variable can take on any real value, positive or negative. Consider the following policy:
Monitor the inventory position 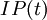 constantly. When
constantly. When 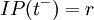 , place a new order of size
, place a new order of size 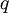 at time
at time 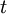 .
.
(The EOQ model's policies are special cases with 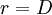 .)
.)
In honor of the two variables, a policy of this kind is called a reorder-point/order-quantity or 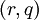 policy.
policy.
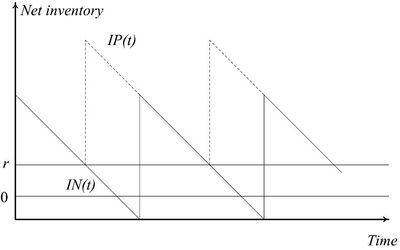
Figure 2 illustrates the behavior of 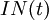 and
and 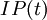 under such a policy.
under such a policy.
As in the EOQ model the graph retains the same sawtooth pattern, but now the pattern can shift vertically, depending on the choice of 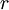 .
.
Performance Criteria
The relevant criteria include average inventory 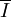 and average frequency
and average frequency  .
.
The primary backorder-related performance measure is the following:
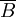 - long-term average outstanding backorders,
- long-term average outstanding backorders,
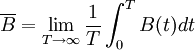
(The limit here is analogous to the one defining 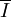 ).
).
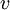 -- safety stock,
-- safety stock,
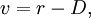
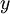 -- safety time,
-- safety time,
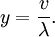
Like 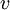 ,
, 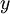 can be negative.
can be negative.
For any given 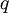 , only certain values of $v$ make sense: Equation (1) implies that the net inventory
, only certain values of $v$ make sense: Equation (1) implies that the net inventory 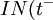 ) just at the end of a cycle is precisely
) just at the end of a cycle is precisely 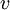 , so
, so 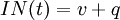 at the beginning of a cycle. Therefore,
at the beginning of a cycle. Therefore,
If 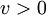 , then for all
, then for all 
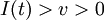 and
and 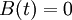
If 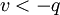 , then for all
, then for all 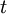
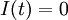 and
and 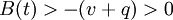
Neither conclusion is appealing: In case 1, we have more inventory than we actually need, and in case 2 we never fill all backorders. So, we can and do restrict attention to the range 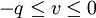 . So,
. So, 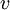 is negative (more precisely, nonpositive), as is
is negative (more precisely, nonpositive), as is 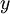 , and each arriving order fills all current backorders.
, and each arriving order fills all current backorders.
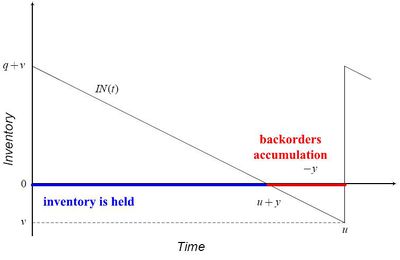
Thus, a cycle consists of two parts, one of length 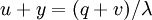 , during which inventory is held, and a second part of length
, during which inventory is held, and a second part of length 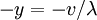 , when backorders accumulate (see fig. 3). These intervals correspond to the fractions
, when backorders accumulate (see fig. 3). These intervals correspond to the fractions 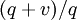 and
and 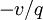 , respectively, of the full cycle.
, respectively, of the full cycle.
The average inventory is simply 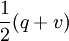 during the first part and zero during the second. The average over a full cycle is a weighted average of these quantities:
during the first part and zero during the second. The average over a full cycle is a weighted average of these quantities:
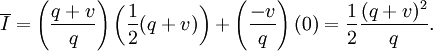
Likewise, the average backorders in the first part of the cycle is zero, and 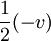 in the second, so
in the second, so
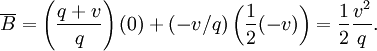
Finally, the cycle length is 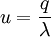 , so
, so
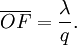
Clearly these criteria are in direct conflict. Let us translate them into monetary terms. We continue to use the cost factors 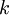 ,
, 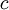 and
and 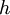 defined earlier. Suppose we can also estimate a factor for backorders analogous to
defined earlier. Suppose we can also estimate a factor for backorders analogous to 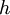 :
:
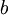 - penalty cost for one unit backordered during one time-unit (moneys/[quantity-unit time-unit])
- penalty cost for one unit backordered during one time-unit (moneys/[quantity-unit time-unit])
This parameter summarizes all the drawbacks of backorders mentioned above. The total average cost then becomes
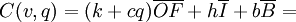
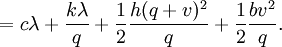
The Optimal Policy and Sensitivity Analysis
The cost 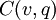 is now a function of two variables. To minimize it, we equate its partial derivatives to zero. (
is now a function of two variables. To minimize it, we equate its partial derivatives to zero. (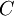 is continuously differentiable and strictly convex on its domain, so this approach works.) That is,
is continuously differentiable and strictly convex on its domain, so this approach works.) That is,
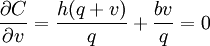
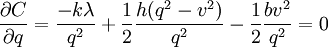
Defining the cost ratio
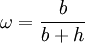
gives the unique solution to these equations as
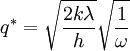
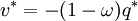
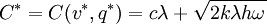
References
- ↑ Zipkin P. (2000) Foundations of inventory management; The McGraw-Hill Companies, Inc.