Load-planning problem
From Supply Chain Management Encyclopedia
Russian: Задача о загрузке самолета
Description of the problem and its solution are based on the method of dynamic programming and Bellman's optimality principle.
Contents |
Dynamic Programming Method
Dynamic programming is widely used in optimal control and planning problems as well as various technical problems.
Suppose that the process of control of a system 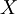 goes
goes  steps. Given a state space
steps. Given a state space 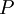 and control space
and control space  with elements
with elements  and
and 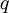 respectively. It is assumed that the initial state
respectively. It is assumed that the initial state  is known. Consider a function
is known. Consider a function  :
:
 , i.e.
, i.e.  .
.
Function  is often referred to as a function of dynamics of the controlled process.
is often referred to as a function of dynamics of the controlled process.
Multi-step guided process is realized as follows (see Fig. 1.)
Step 1. The system is in the state  . In this state the following control is used
. In this state the following control is used  . Mapping
. Mapping  sets the system into a new state
sets the system into a new state 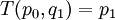 .
.
Step 2. The system is in the state  . In this state the following control is used
. In this state the following control is used  so
so  .
.
Step k'. The system is in the state  . In this state the following control is used
. In this state the following control is used  , then
, then  .
.
Stepn. The system 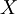 is in the state
is in the state  . When the control
. When the control  is chosen we have
is chosen we have  . The process ends.
. The process ends.
Fig. 1. The implementation of the multi-step control process.
We denote  - multistep control process. Then this initial state
- multistep control process. Then this initial state  and control
and control 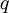 corresponds to a trajectory
corresponds to a trajectory  , where
, where  ,
, 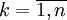 .
.
Assume that on control 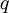 and trajectory
and trajectory  is given an additive function:
is given an additive function:
 .
.
Denote
 .
.
value of the function  on the trajectory of the process from the initial state
on the trajectory of the process from the initial state  in
in 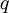 .
.
Now we can formulate the discrete optimal control problem. Find the optimal control  , which is the solution of the following problem:
, which is the solution of the following problem:
![\, \mathop{\max }\limits_{q} K(p_{0} ,q)=\max \left[\sum _{i=1}^{n}f_{i} (p_{i-1} ,q_{i} ) +f_{n+1} (p_{n} )\right]](/images/math/3/a/e/3aee21423e2c4c3fcc8a6feaffe7a582.png) .
.
under dynamic constraints:

where  - given initial state of the process.
- given initial state of the process.
Note that when the control 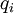 is being choosing in step
is being choosing in step  we know the state of the process
we know the state of the process  in the previous step, and the knowledge of
in the previous step, and the knowledge of  defines the future state of the process and the value of the functional. It is therefore natural to consider functions
defines the future state of the process and the value of the functional. It is therefore natural to consider functions  ,
,  and set of functions
and set of functions
(1) 
where  . Such set of functions
. Such set of functions  is called a strategy.
is called a strategy.
Bellman's Optimality Principle
Optimal strategy

has the property that whatever the initial state  and the initial control is chosen
and the initial control is chosen  , it remains the best strategy in the process with
, it remains the best strategy in the process with  steps, which starts at the state
steps, which starts at the state  .
.
From Bellman's optimality principle can be derived recurrence functional Bellman equation, which is the basis of computational procedures for dynamic programming.
Denote  - the maximum functional value in
- the maximum functional value in  - steps problem from the initial state
- steps problem from the initial state  . Function
. Function  is often called the Bellman’s function. From the principle of optimality we have the following equation.
is often called the Bellman’s function. From the principle of optimality we have the following equation.
The Bellman Equation
(2) 
with the boundary condition

The general scheme of dynamic programming
Consider the idea of dynamic programming in the following example. Find:
(3)  ,
,
 ,
, 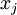 - integer,
- integer,  .
.
Because the variables 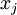 ,
,  are independent, then
are independent, then
![\, \mathop{\max }\limits_{x_{1} ,...,x_{n} } \sum _{j=1}^{n}f_{j} (x_{j} ) =\mathop{\max }\limits_{x_{n} } \left[f_{n} (x_{n} )+\mathop{\max }\limits_{x_{1} ,...,x_{n-1} } \sum _{j=1}^{n-1}f_{j} (x_{j} ) \right]](/images/math/3/d/0/3d0a6a38984c33b48f049b503da8dc75.png) ,
,
(4) 
Denote  in the condition (4) through
in the condition (4) through  , then
, then
(6) ![\, \mathop{\max }\limits_{x_{1} ,...,x_{n} } \sum _{j=1}^{n}f_{j} (x_{j} ) =\mathop{\max }\limits_{x_{n} } \left[f_{n} (x_{n} )+F_{n-1} (b-a_{n} x_{n} )\right]](/images/math/2/6/0/260128df688d7763e80b4874089cdb27.png)
Denote  under condition
under condition
 .
.
 ,
, 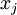 - integer,
- integer,  .
.
After transformations we obtain the following fundamental recurrence relation of dynamic programming
(7) ![\, F_{k} (\xi )=\mathop{\max }\limits_{x_{k} } \left[f_{k} (x_{k} )+F_{n-1} (\xi -a_{n} x_{n} )\right],\, \, \, k=\overline{1,n}](/images/math/a/3/9/a39dcea14b5d1526b75eb91d9bc02da1.png)
subject to  .
.
Use (7) to define calculation process:
Construction of Bellman’s function.
Step 1. Compute
(8)  ,
,
where  - a parameter of the process. Fill the table 1 by values
- a parameter of the process. Fill the table 1 by values  ,
, 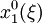 , for
, for 
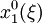 - optimal solution of the problem (8).
- optimal solution of the problem (8).
Step 2. Compute
(9) ![\, F_{2}(\xi )=\mathop{\max }\limits_{0\le x_{2} \le \frac{\xi }{a_{2}}} \left[f_{2}(x_{2})+F_{1}(\xi-a_{2} x_{2})\right]](/images/math/5/c/7/5c7335c5c45119063d83d8cdf283a4b0.png)
Values  for different values of the argument
for different values of the argument  select from Table. 1. Fill in the table 2 with the following results:
select from Table. 1. Fill in the table 2 with the following results:  ,
,  , where
, where  - the optimal solution of problem (9).
- the optimal solution of problem (9).
Step k.  . Compute
. Compute
(10) ![\, F_{k}(\xi )=\mathop{\max }\limits_{0\le x_{k} \le \frac{\xi}{a_{k}}} \left[f_{k}(x_{k})+F_{k-1}(\xi-a_{k}x_{k})\right]](/images/math/b/9/2/b92d41025d3dbbc76f81d73a99585dd4.png)
Fill in the table of values  ,
,  ,
,  , where
, where  - the optimal solution of problem (10).
- the optimal solution of problem (10).
Optimal solution computation.
Assuming  and
and  find
find  and
and  .
.
Calculate in (10) the optimal value  and assume
and assume  . Then, using the value of
. Then, using the value of  of the table step
of the table step  , determine the optimal values of other variables
, determine the optimal values of other variables  . Then determine the values
. Then determine the values  .
.
 |  | 
|
 |  | 
|
 |  | 
|
 |  | 
|
 |  | 
|
 |  | 
|
Table 1. Table for the first iteration
 |  | 
|
 |  | 
|
 |  | 
|
 |  | 
|
 |  | 
|
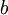 |  | 
|
Table 2. Table for the second iteration
To apply dynamic programming method the following conditions are to be satisfied:
- The decision-making process should allow an interpretation as a multi-step process;
- For each step it should be defined a set of state parameters
 , which do not depend on the number of steps;
, which do not depend on the number of steps;
- Optimal solution in step
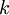 depends only on the current state and does not depend on the prehistory of the process.
depends only on the current state and does not depend on the prehistory of the process.
Aircraft Loading Problem
An aircraft is loaded by objects  of various types. Each object type
of various types. Each object type  has weight
has weight  and insurance cost
and insurance cost  , (
, ( ). Maximum load capacity of the aircraft is
). Maximum load capacity of the aircraft is  . It is required to determine the maximum value of the goods whose weight must not exceed maximum permissible carrying capacity of aircraft. For definiteness, assume that
. It is required to determine the maximum value of the goods whose weight must not exceed maximum permissible carrying capacity of aircraft. For definiteness, assume that  and there are three types of objects, details of which are listed in the table below:
and there are three types of objects, details of which are listed in the table below:
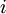 |  | 
|
 |  | 
|
 |  | 
|
 |  | 
|
Consider the problem in general formulation. Denote the number of items such as  by
by  . Then the problem of loading the aircraft can be written as:
. Then the problem of loading the aircraft can be written as:


where 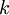 are integer.
are integer.
If it were possible to discard the requirement of integrality, it was a linear programming problem and it could be solved with the simplex method.
Consider three main elements of a dynamic model.
1. Step  is associated with type
is associated with type 
2. State  on stage
on stage  is the total weight of items, loaded on the previous stages
is the total weight of items, loaded on the previous stages 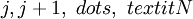 . The variable
. The variable  can be
can be  in
in  .
.
3. Solutions. Values 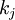 on stage
on stage  describe the type of items
describe the type of items  . Value
. Value ![\, k_ {j} \ in [0, [W / F_ {j}]]](/images/math/3/6/2/362780a1a3fd80272ddd9b032a62d154.png) , where
, where ![\, [W / F_ {j}]](/images/math/c/2/7/c275cfd21648c118bd427358b4583605.png) is the integral part of
is the integral part of  .
.
Let  is maximum total value of items loaded in phases
is maximum total value of items loaded in phases  for a given state
for a given state  .
.
The recurrence relation is the following:

![\,f_{j} (y_{j} )=\mathop{\max }\limits_{\begin{array}{l} {k_{j} =0,1,...,[W/F_{j} ]} \\ {v_{j} =0,1,...,W} \end{array}} \{ v_{j} y_{j} +f_{j+1} (y_{j} -F_{j} k_{j} )\} ,\, \, \, \, j=1,2,...,N-1](/images/math/8/f/c/8fced00ee70af3a266e6c749db3d8aff.png)
The maximum value 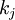 is bounded by
is bounded by  .
.
Example
For our example, calculations begin with the third stage and are performed as follows.
Stage 3.
![\,f_{3} (y_{3})=\mathop{\max }\limits_{k_{3}} (30k_{3}), \max k_{3}=[5/1]=5](/images/math/9/8/8/9883bfe7ea4af47c97f4d5cd4e814b2a.png)
Stage 2.
![\,f_{2} (y_{2} )=\mathop{\max }\limits_{k_{2} } (80k_{3} +f_{2} (y_{2} +3k_{2} )), \max k_{2} =[5/3]=1](/images/math/d/b/f/dbf8be46f896a1c4f29373608ad6c40c.png)
Values in columns are obtained using the recurrence relations. For example, the value in the column  in
in  is obtained as follows:
is obtained as follows:
 ,
,
because from the table of step 3,  .
.
Stage 1.
![\,f_{1} (y_{1} )=\mathop{\max }\limits_{k_{1} } (65k_{1} +f_{2} (y_{1} +2k_{1} )), \max k_{1} =[5/2]=1](/images/math/2/7/9/27940926a1c1f36446f6e5412eba9ee7.png)
For a given  the optimal solution is
the optimal solution is  , and the total value of goods is equal to 160.
, and the total value of goods is equal to 160.








