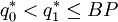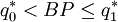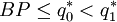Incremental Discounts
From Supply Chain Management Encyclopedia
Russian: Экономичный размер заказа с учетом скидки за прирост
In the Basic economic order quantity (EOQ) model the variable cost 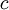 is constant for orders of all sizes. However, it is common for suppliers to offer price breaks for large orders. This section shows how to extend the EOQ model to incorporate such quantity discounts. Actually, there are two kinds of discounts, incremental and all-units[1].
is constant for orders of all sizes. However, it is common for suppliers to offer price breaks for large orders. This section shows how to extend the EOQ model to incorporate such quantity discounts. Actually, there are two kinds of discounts, incremental and all-units[1].
Consider the first case: Suppose the purchase price changes at the breakpoint 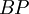
The variable cost is 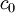 for any amount up to
for any amount up to 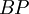 . For an order larger than
. For an order larger than 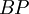 , the additional amount over
, the additional amount over 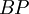 incurs the rate
incurs the rate 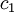 where
where 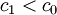 .
.
Thus, the total order cost is
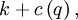
where
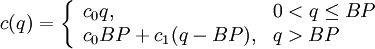
Alternatively, define 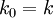 (a constant) and
(a constant) and 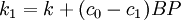 (a constant!). Then, the order cost is
(a constant!). Then, the order cost is
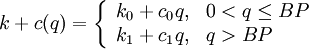
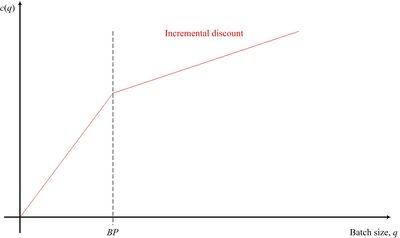
This function describes more elaborate economies of scale than the original fixed-plus-linear form. In a production setting, it represents costs that depend on the production quantity in a complex, nonlinear way.
The figure illustrates 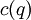 for the incremental case.
for the incremental case.
Given the revised order cost for the incremental case, the formulation proceeds as in the EOQ model. The holding cost is a bit tricky, however.
In addition to direct handling costs, which occur at rate 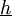 , there is also a financing cost, which occurs at rate
, there is also a financing cost, which occurs at rate 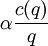 .
.
Here, 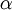 is the interest rate, and
is the interest rate, and 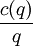 is the average variable purchase cost. Thus, the total average cost is
is the average variable purchase cost. Thus, the total average cost is
![\,C(q)=\left[k+c(q)\right]\cdot \frac{\lambda }{q} +q\cdot \frac{1}{2} \cdot \left[\underline{h}+\alpha \cdot \frac{c(q)}{q} \right]](/images/math/4/f/a/4faa90a09d8be0549abcca49a234d5e6.png)
(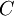 is not differentiable at
is not differentiable at 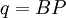 , so we cannot hope simply to differentiate to obtain the optimal solution. Also,
, so we cannot hope simply to differentiate to obtain the optimal solution. Also, 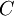 is not convex.)
is not convex.)
Observe that
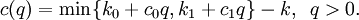
That is, 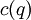 is the smaller of two positive, linear functions that cross at
is the smaller of two positive, linear functions that cross at 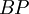 . Therefore,
. Therefore,
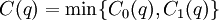
where
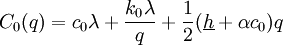
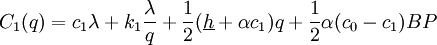
Both 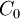 and
and 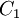 have the form of the EOQ model's cost function. Both are strictly convex and differentiable, and their graphs cross at
have the form of the EOQ model's cost function. Both are strictly convex and differentiable, and their graphs cross at 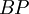 . Let
. Let 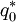 and
and 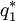 be the respective minimizing values of
be the respective minimizing values of 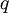 . Also,
. Also,
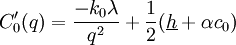
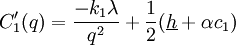
Evidently, 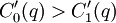 , so
, so 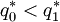 . There remain three possible cases:
. There remain three possible cases:
In case 1, for 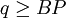 ,
,
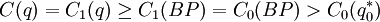
so 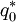 is optimal. In case 3, by a parallel argument,
is optimal. In case 3, by a parallel argument, 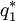 is optimal. Only in case 2 is there any doubt. In that case, calculate both
is optimal. Only in case 2 is there any doubt. In that case, calculate both 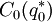 and
and 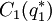 to determine which one is smaller.
to determine which one is smaller.
In sum, it is easy to determine an optimal policy: Compute both 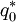 and
and 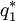 using EOQ-like formulas, compare them with
using EOQ-like formulas, compare them with 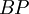 to determine which case applies, and if necessary (in case 2) compare their costs.
to determine which case applies, and if necessary (in case 2) compare their costs.
References
- ↑ Zipkin P. (2000) Foundations of inventory management; The McGraw-Hill Companies, Inc.