Financial logistics
From Supply Chain Management Encyclopedia
Russian: Финансовая логистика
The purpose of financial logistics is to apply financial and accounting tools to solving supply chain problems and to making the business case for investments in a firm's supply chain infrastructure. The tools and knowledge required to sucessfuly use financial logistics include:
- Net present value: What it is and how to apply it;
- Income statements and balance sheets (see selecting the customer service level for an example of the use of an income statement in selecting the optimal on-time delivery rate);
- The cash-to-cash cycle and order-to-cash cycle;
- The inventory carrying cost rate and it use and application;
- Financial performance metrics including return on investment (ROI) which is decribed below.[1]
Not all these tools and knowledge issues are required in every situation and often the data required for soving a problem may come from many different sources. Here we shall provide one example of how some of these elements may come together in solving a specific supply chain problem.
Contents |
Example
Suppose that a clothing retail company is vertically integrated and involved in many, but not all, supply chain stages ranging from product design through to retailing the product at its own stores under its own brand name. The general process involved is provided in the Figure. The design of product occurs at corporate headquarters in New York City. Designers also select product materials and fabrics. Materials in the form bolts are acquired from many sources located in the United States, Europe (notably Italy), and Asia and then shipped to factories located in East Asia, the Carribean, and Oceania. The retailer outsources all production to third party manufacturers, however, the company has a long history with these firms and is highly involved in supervising quality control. The finished product is then shipped to the company's distribution center. The retail outlets are located only in the United States, therefore this single facility is cost and service effective. All product inbound from foreign manufacturing facilities arrives at the single distribution center. Product is unloaded from containers and putaway into storage. Planners in New York City then allocate product to the various stores. These orders result in a picking and packing process at the distribution center and the loading of product onto motor carrier trailers. Shipments at this stage are not direct to the retail outlets. Rather, to take advantage of truckload rates, full truckloads are shipped to various deconsolidation points where local distributors then deliver product to the retail outlets. Deconsolidators and local delivery are performed by third party, contract operators. The entire process from design to store arrival is planned in 48 week cycles. The process is built around the required in-store date. All other dates are built sequentially backwards on a stage by stage basis. For example, product is shipped from the central distrbution center to local deconsolidators seven days before the in-store date. This provides a two-day buffer for the deconsolidators in case truckload shipments are delayed due to unexpected events (or variance in shipment time). These buffers are built into into every stage in the process to accomodate variation in the amount of time required for any stage to be completed.
The retailer is considering changing the point at which product is allocated to the retail outlets. Supply chain managers would like the allocation planning team to shift the point to the stage where the product is en-route from the manufacturers to the distribution center. This would allow the distribution center to shift from operating primarily as a warehouse to primarily as a flow through facility. The loading and unloading functions at the distribution center would remain. However, the putaway, storage, and picking and packing functions would be greatly diminished. Allocating prior to arrival at the distribution center would allow for product to be cross-docked: i.e., product would be unloaded from an inbound dock and immediately transferred to an outbound dock and loaded onto the approariate trailer for shipment to a local deconsolidator. Only 90% of the product would be handled in this fashion. The remaining 10% of product would be stored to accomodate unexpected demand from specific retail outlets and/or regions. This is equivalent to safety stock that is used to satisfy unexpected changes in demand. The key facts required to assess the proposal include:
- The proposal would eliminate, on average, about 14 days worth of time from the supply chain, bringing the 48 week total planning cycle down to 46 weeks. The inventory carrying cost rate across all products is 30 percent. The average replacement value of inventory in the system is about $75 million.
- Fewer warehouse personnel would be required. The staff involved in warehouse operations (not management) would fall from about 500 to 300. The total compensation package per staff member is about US $30,000 which includes both wages and required employer contributions: e.g., social taxes for retirement plans, unemployement benefits.
- The internal configuration of the warehouse would require reconstruction. A flow flow through facility requires a set of conveyors with attendant bar code scanners. Boxed inbound inventory would be put through the mechanical sortation system and arrive at the correct outbound bay. A new system of this sort is expected to cost about US $13 million. Annual expenditures on repair and maintenance would cost about US $300,000. An annual increase in the utility bill of US $100,000 is expected.
- Additional expenses would be incurred in monitoring and enforcing supplier standards in terms of carton dimensions and weight. These are important as oversized cartons will not be able to fit onto the mechanical sortation system and will require additional physical handling. Penalties will be applied to suppliers who ship product that is out of specification. The penalties are not designed so much to recoup additonal expenses are they are deter suppliers from contract non-compliance. The annual cost of the new enforcement system is expected to be about $50,000. The retailer was not able to estimate revenue from penalities in advance.
- Currently, when a container of product arrives at the distribution center it is typically unloaded within two days. Under the new system, containers are expected to sit in the yard for an average of four days. These additional two days are already included in the 14 day reduction from the supply chain. However, the company is expected to incur US $30,000 in annual penalties from container owners. The yard will have to be reconfigured at a cost of US $500,000 and an addtional annual expense in yard operations is expected to be incurred at a rate of US $100,000 per year.
- In reality, a number of other factors are involved. Expenses will continue to be incurred on the 10% of inventory that is put away as safety stock. Allocating earlier in the supply chain decreases the ability of planners to match supply to anticipated demand and such mismatches may results in a higher level of markdowns at the retail outlets. A number of other factors will not affect the analysis as they will remain constant regardless of whether the proposal is accepted or not. For example, the distribution center supports new store openings (e.g., racks, inventory, signage) and this function is independent of the allocation point.
- A simplified version of the income statement and balance sheets are provided below.
Issues Critical to Upper Management
Three measures are desired to assist senior managers in making the decision as to whether to shift the allocation point:
- What is the return on investment?
- What is the net present value?
- What is the implied rate of return?
Applying Financial Logistics to the Problem: Simple ROI
Return on investment (ROI) is one of several approaches for evaluating the financial concequences of a potential investment. The approach considers the timing and magnitude of both gains (or money inflows) as well as costs (or money outflows). The higher the ROI, the more appealing the investment. Typically, projects compete for funds and the ROI has therefore becomes a tool for evaluating alternative investments by the firm. In the problem we analyze, we limit ourselves to a single investment in isolation. One shortcoming of both the ROI and NPV approaches is that they do not account for risk. They evaluate the expected return or value. For this reason, ROI and NPV analyses may be supplemented with sensitivity analysis, potentially showing best and worse case scenarios. The formula for the simple (non-discounted) ROI is:
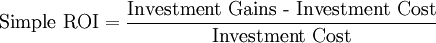
The basic inputs for the allocation timing problem are:
- Initial cost (or initial cash outflow) = Conveyor Investment + Yard Reconfiguration = US $13 million + $500,000 = $13.5 million
- Annual cost (or annual cash outflows):
- = Enforcement + Yard Expenses + Container Fees + Conveyor Upkeep + Utilities
- = $50,000 +$100,000 + $30,000 + $300,000 + $100,000 = $580,000
- Annual gains (or annual cash inflow):
- = Labor + Inventory Cost
- Labor 200 employees at $30,000 = $6 million
- Inventory savings = 14 days of inventory = inventory carring cost rate (c) × replacement value of inventory (v) × 14 / 365 = .30 × $75 million × 14 / 365 = $863,000
- = $6 million + $863,000 = $6.863 million
- = Labor + Inventory Cost
The next step in the simple ROI analysis is to build a table showing gains and costs across time. As seen in Table 1, the gains (or cash inflow) equals zero in year zero and then equal $6.863 million every year after that (the gains equal the savings in the inventory vcarrying cost and in distribution center labor reduction). The cost (or cash outflow) is $13.5 millionn in year zero (which equals the cost of the conveyor system plus yard reconfiguration). Every year after that, the cost equals $580,000 (or the sum of enforcement, yard expenses, container fees, conveyor upkeep, and additional utilities). The next line, or net cash flow, equal the gain for a particular year minues the cost. The cumulative cash flow represents the additive stream of cost minus gain for any given year. Finally, the Simple RIO is evaluated using the provided formula. For example for Year 3:
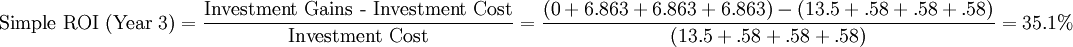
| Table 1: Simple (Non-discounted) ROI Analysis ($'000) | ||||||
|---|---|---|---|---|---|---|
| Year 0 | Year 1 | Year 2 | Year 3 | Year 4 | Year 5 | |
| Gains (cash inflow) | 0 | 6.863 | 6.863 | 6.863 | 6.863 | 6.863 |
| Cost (cash outflow) | 13,500 | .580 | .580 | .580 | .580 | .580 |
| Net cash flow | -13,500 | 6.283 | 6.283 | 6.283 | 6.283 | 6.283 |
| Cumulative cash flow | -13,500 | -7.217 | -.934 | 5.349 | 11.632 | 17.915 |
| Simple ROI | -100.0% | -51.3% | -6.4% | 35.1% | 73.5% | 109.2% |
Discounted ROI and NPV
A shortcoming Simple ROI is that it does not discount the future value of money. Suppose we use a discount rate of 6% and revaluate the ROI. The first row in Table 2 shows the denominator that is utilized in the NPV model. It is simply 1.06 raised to the power of the year. Thus the value for year 3 is 1.06³=1.191. Each entry in the gains (cash inflow) row and in the cost (cash outflow) rown is dvidied by the respective discount value. For example, the gain for Year 3 is 5.762 = 6.863 / 1.191 while the cost for year 3 is .487 = .580 / 1.191. The net cash flow, cumulative cash flow, and Discounted ROI are evaluated as they were in the Simple ROI analysis. For example the Discounted ROI for Year 2 equals:

| Table 2: ROI Analysis ($'000) with a 6% Discount Rate | ||||||
|---|---|---|---|---|---|---|
| Year 0 | Year 1 | Year 2 | Year 3 | Year 4 | Year 5 | |
Time value of money =  | 1.000 | 1.060 | 1.124 | 1.191 | 1.262 | 1.338 |
| Gains (cash inflow) | 0 | 6.475 | 6.108 | 5.762 | 5.436 | 5.128 |
| Cost (cash outflow) | 13,500 | .547 | .516 | .487 | .459 | .433 |
| Net cash flow | -13,500 | 5.927 | 5.592 | 5.275 | 4.977 | 4.695 |
| Cumulative cash flow (NPV) | -13,500 | -7.573 | -1.981 | 3.295 | 8.271 | 12.966 |
| Discounted ROI | -100.0% | -53.9% | -13.6% | 21.9% | 53.3% | 81.3% |
The effect of discounting the investment cost and gains is to lower the ROI across time. Finally, a net present value model may be applied to the problem. In this case, the cumulative cash flow equals the NPV as it represents the sum of the initial investment (expressed as a neagtive number) plus the discounted difference between the investment cost and gains. The NPV equals -$7.572 million after Year 1. By Year 3, the NPV is positive ($3.295 million) and remains so through Year 5. The implied rate of return is the discount rate at which the NPV equals zero. The implied rate of return will vary with the length of the planning horizon. In this case, a discount rate of 36.8% will provide an NPV=0 for the 5 year horizon. The fiancial analysis of the proposal to shift the allocation point looks promising: (1) The discounted ROI (using a 6% discount rate) equals 81.3% over a five year horizon; and (2) the NPV for the same period US $12.966 million. Naturally, this investment must be weighed against others that the firm is considering, and risk must be assesed, however, when considered in isolation, the investment looks worthwhile.
References
- ↑ Moyer, R.C., J.McGuigan and W. Kretlow (2006), Contemporary Financial Management, Mason, OH: South-Western Publishing.





