EOQ with price gap
From Supply Chain Management Encyclopedia
Russian: Экономичный размер запаса с разрывами цен
Consider the case of static demand.
The Basic Assumptions of the Model
- Number of units consumed per unit of time is a constant (demand rate);
- Price of the resource unit depends on order volume. If the order quantity does not exceed a certain level of
 , then the price is constant
, then the price is constant 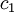 , otherwise - the price is a constant
, otherwise - the price is a constant  , where
, where  :
:

- Carrying cost of resource unit is a constant;
- Order cost is a constant;
- Lead time is zero.
The Basic Notation
-
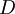 – demand rate;
– demand rate;
-
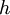 – marginal carrying costs;
– marginal carrying costs;
-
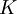 – fixed order costs;
– fixed order costs;
-
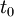 – order cycle time;
– order cycle time;
-
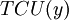 – total costs per unit of time;
– total costs per unit of time;
-
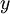 – order quantity;
– order quantity;
-
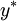 – economic order quantity.
– economic order quantity.
Inventory Optimal Control
Costs of resource per unit of time are a function of the size of orders:

Given the dependence of the order cycle time on the intensity of demand for the resource, 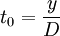 , the cost of the purchase of products per unit time can be represented as:
, the cost of the purchase of products per unit time can be represented as:

The total cost per unit time can be represented as a function of order volume 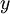 as the sum of acquisition costs of resource per unit of time, the cost of ordering and storage costs of the resource per unit time:
as the sum of acquisition costs of resource per unit of time, the cost of ordering and storage costs of the resource per unit time:

or:

The graphs of the function  and
and  are the following, fig. 1:
are the following, fig. 1:
Fig. 1. The function of total costs
The point  is determined according to economic order quantity:
is determined according to economic order quantity:
 .
.
In the point  the following inequality holds:
the following inequality holds:
 ,
,
or:
 ,
,
then:
 .
.
When  graph
graph 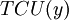 equal to
equal to  . When
. When  graph
graph 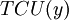 equal to
equal to  . In correspondence with a graph, consider the three areas on the x-axis:
. In correspondence with a graph, consider the three areas on the x-axis:  ,
,  ,
,  , which are called, respectively: A, B and C. The optimum size of the order
, which are called, respectively: A, B and C. The optimum size of the order 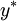 depends on what area is the point
depends on what area is the point  , Fig. 2, 3, 4:
, Fig. 2, 3, 4:

Fig. 2.  ,
,  .
.
Fig. 3. 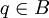 ,
,  .
.
Fig. 4.  ,
,  .
.
Optimal inventory control in the model is the following:
Step 1. According to EOQ compute  . If
. If  , then
, then  , else, go to step 2.
, else, go to step 2.
Step 2. Compute  from the following equation:
from the following equation:
 ,
,
to determine the border areas  and
and 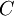 . If
. If 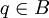 , then
, then  , if
, if  , then
, then  .
.








